The Kelly Criterion
The Kelly Criterion is a widely discussed topic in gambling circles, especially on platforms like X (formerly Twitter). In my opinion, it is also one of the most misunderstood. Some view it merely as a useful formula for bet sizing, while others completely disregard it, both groups often without considering its deeper meaning, implications and applications. I understand that most gamblers likely haven’t read Kelly’s original paper, but I have, and despite much of it being Greek to me, I have thought a lot about it and believe I have identified a few crucial aspects of successful gambling that align well with Kelly’s original intentions.
EV Isn’t Everything
Expected Value (EV) is another often misunderstood concept, and its importance is often overemphasized. While it is a measure of our edge, it’s not enough to fully describe a bet, and it’s not the only factor considered in the Kelly Criterion. What Kelly tells us is that the probability of winning, or rather not losing, is at least as important for successful (long-term) gambling.
Imagine two bets, both with 10% EV: one with a win probability of 0.10 and one with 0.50. Kelly favors the bet with higher win probability and suggests betting more on it. Why?
The answer is that maximizing our EV on any individual bet isn’t the goal of successful gambling. Studying Kelly helps us understand that focusing too much on EV is a sure way to go broke. Yes, we only want to place positive EV bets (actually not true, as you’ll soon see), but focusing on not losing rather than trying to maximize our payoff is at least as important. This is because all bets come with a risk of losing, and over time we will lose, not just once but many times in a row. Brutal downswings are a natural part of gambling, so even if we have an edge, we don’t want to overbet (trying to maximize our EV) as we risk getting wiped out.
Consider a bet with a favorable edge: someone offers you a fair coin flip at 2.1 odds over 100 bets with the following conditions:
- You have to bet on all 100 coin flips.
- Your starting bankroll is 100 units.
- You must decide beforehand what fraction of your bankroll should be bet on each coin flip.
- If your bankroll falls below what you’d bet with a 100 unit bankroll, you’ll have to borrow what you need to get back to 100 units.
The EV for this proposition is clearly positive, but if you focus solely on EV and try to maximize it (that would mean going all-in on every bet), you are in for a painful surprise.
Take a good look at the plot above. Then take another good look. Sure, this is only one of infinitely many runouts of our little proposition, but the results are clear: even though we maximize our EV by betting our whole bankroll on each coin flip, any loss forces us to borrow another 100 units to continue wagering. The result of our overbetting is a deep hole of debt we cannot escape while still betting this way. Our EV increases with every coin flip, and we sometimes see winning streaks temporarily lifting us out of the hole. However, by severely misbalancing risk and reward, we are bound to end up losing.
Ok, ok, ok. So we have to bet less to give us a better chance of staying in the game and realize what should be a fairly profitable situation. What if we decide to bet half our bankroll on each coin flip? Well, take a look:
At least the hole is not as deep this time, but it’s still clear we are betting too much. Even with steadily growing EV and some winning streaks, we still end up losing and in debt. Again, remember that the above is just one of many possible paths our betting could take.
But what if we go even more conservative and bet only a quarter of our bankroll? Surely we should have a much better chance of realizing our edge then? Yes, over 100 flips we might get lucky and quit ahead, but in the long run we are still overbetting and heading for ruin. Here’s one example of the results of flipping 1000 coins:
It is very hard to escape the ruin of overstaking. By now it should be obvious that staking correctly is just as important as finding the +EV bet in the first place. Maybe even more important as like we’ve seen again and again now, a solid edge will be for nothing if we stake too much. So we should use the Kelly Criterion.
Enter Ergodicity
Ergodicity is key to understanding the Kelly Criterion. If a process (such as betting on 100 coin flips) is ergodic, it means the long-term outcome of the series of bets is the sum of the individual EVs. For us this isn’t true because our bets are not made in isolation. In fact, they are very dependent on each other, as the result of the previous bet determines how much we can bet on the next. In most situations, if we bet everything and lose, we won’t be able to bet next time. But if we win, we can wager much more on the next bet. Thus, our betting proposition is non-ergodic.
The 8th Wonder of the World
Albert Einstein reportedly called compound interest the “8th wonder of the world”. The Kelly Criterion leverages this principle by suggesting a strategy that maximizes the growth rate of your capital over time. This is achieved not by going all-in when we have an edge, but by using our bankroll in a way that balances risk and reward to utilize the power of compounding.
Take a look at the above plot. We are now betting the optimal amount on each bet according to Kelly. The key difference here is that since we are always betting just a fraction of our bankroll, we never end up losing enough to get into debt. This, of course, assumes our bankroll is infinitely divisible, and though it sounds silly, it’s almost correct in today’s gambling world. You can bet a few dollars, euros, pounds, or even cents or pennies with most online bookies. Hopefully, we won’t ever be in that situation, and if we are, we will hopefully be able to replenish our bankroll to get back to more rewarding bet sizes.
Another striking difference from going all-in on every bet is that we are actually winning here. This is because even after losing we can always bet a reasonable amount on the next bet and eventually realize our positive EV. We also see that 100 bets aren’t that many, and even when betting full Kelly (which many gamblers avoid because of the swings that come with it), not much is really happening here. Sure, we are winning, but we can’t afford to retire. Yet.
So what if we agree to bet 1000 coin flips instead? Well, now we are approaching long run territory, and with full Kelly we are in for a wild ride:
The above example highlights two key points of full Kelly betting: first, we are starting to see that nice exponential growth that we hope will eventually allow us to retire, but we also see it comes with some nasty downswings that few gamblers are willing to stomach. Remember, this is a situation where we know we have an edge. But what if we couldn’t be 100% sure we have an edge, how would we feel about losing half our bankroll in quick succession, or long, painful streaks of barely breaking even? How sure can we be that we actually are doing the right thing then? If they could, many would surely decide to quit and thus risk missing out on future profits.
Full Kelly betting is optimal in the long run, but the wild ride certainly isn’t for everyone. If we can’t stomach the swings, instead of quitting, it would be better to bet just a fraction of the Kelly optimal stakes to improve our chances of staying in the game. This approach would allow for an easier ride and enable us to still realize some profits without the stress-induced ulcers. It will also protect us from being overconfident in our projected numbers. Remember that overbetting is bad and can make our bankroll turn into dust even with a solid edge like our coin-flipping example. In the real world, most probabilities aren’t known but are just approximations, so it’s wise to be a bit conservative and sacrifice some potential value for a lower risk of ruin.
Many gamblers use quarter Kelly stakes, betting just 25% of the optimal amount. You can see in the plot above that this likely won’t return as much profit as full Kelly, but the growth is steadier and the downswings are easier to cope with. But if we are in for the long run, even quarter Kelly will eventually see us increase our bankroll manifold. In the end, it’s a matter of how sure you can be of your edge, how long you think you can keep betting until it disappears, and how much risk and volatility you think you can handle. All these factors are highly individual, so there’s really no right way of sizing your bets. But there are a lot of wrong ways.
Moving Beyond the Famous Formula
There’s still one very important aspect of the Kelly betting left to discuss. It’s the punchline, the final piece of evidence that will drive home the point and win the case for the Kelly Criterion as the best way to manage your bankroll.
What if, just as you are deciding what Kelly fraction to stake on the above proposition, some weirdo offers you the option to bet the opposite side of each coin flip with them at odds of 1.95? You realize this is an arbitrage opportunity but why would you give up a solid 5% edge and throw away your money just to achieve a small 1.11% arb by hedging the other side of the flip at 1.95? You laugh at the idea. It must be a joke, right? Right?
Actually, saying no to this negative EV bet is a huge mistake. Why? Because the essence of the Kelly Criterion - maximizing long-term growth - isn’t about any single bet. We’ve seen this before when discussing compounding a long series of bets, but it’s also true for each individual coin flip. The Kelly Criterion, when applied correctly, will search for any possible combination of stakes on any possible outcomes to reach the optimal position for each flip. But negative EV is negative EV, right? Hold on.
Take a look at the above plot. What it shows is the expected log bankroll for different stake sizes and two different staking strategies:
- Single Stake - full Kelly on just the value side
- Split Stakes - staking one part of your bankroll on the value side and the other as a hedge on the -EV side, putting your whole bankroll into action
If you are confused by the log part, just ignore and look at the plot the same way you would if it was just expected bankroll, without the log. Higher is better.
When we allow Kelly to bet any stake on any outcome, what it finds is that for this particular example, the staking plan that gives us the highest expected log bankroll (optimal long term bankroll growth) is placing 50 units on the value side and 50 units on the -EV hedge side, resulting in an expected log bankroll of about 4.617. Compare this to the vanilla Single Stake Kelly, placing 4.55 units on just the value side, resulting in an expected log bankroll of 4.616. Both options have been highlighted in the plot, together with the arb option - 48.15 on the value side, 51.85 on the hedge, resulting in an expected log bankroll of about 4.606. The differences in log values are increadibly small but as we will see later on, in real money it’s much more clear.
But how can we achieve optimal bankroll growth by making -EV bets? Firstly, putting our whole bankroll into action by splitting the stakes and hedging opens up for faster compounding, just like the arbitrage option. In fact, the arbitrage option is just a Split Stakes strategy set to return the same amount on both outcomes. In this particular case it just happens that a 50/50 split is better. Secondly, we are no longer betting on odds of 2.1. In fact, when splitting our stakes 50/50 on odds 2.1 and 1.95, we are now only risking 2.5 units to gain 5 - odds of 3.0! So by hedging correctly, we are actually risking less to win basically the same amount. It should now be obvious that this is clearly the optimal strategy here. It should also be noted that the Split Stakes strategy is only the best option when there’s an arb like we have here. With no arb, we are better off just betting full Kelly on the value side.
Still not convinced? Ok, let’s set up the three strategies to bet the exact same coin flips and we’ll see which is most successful.
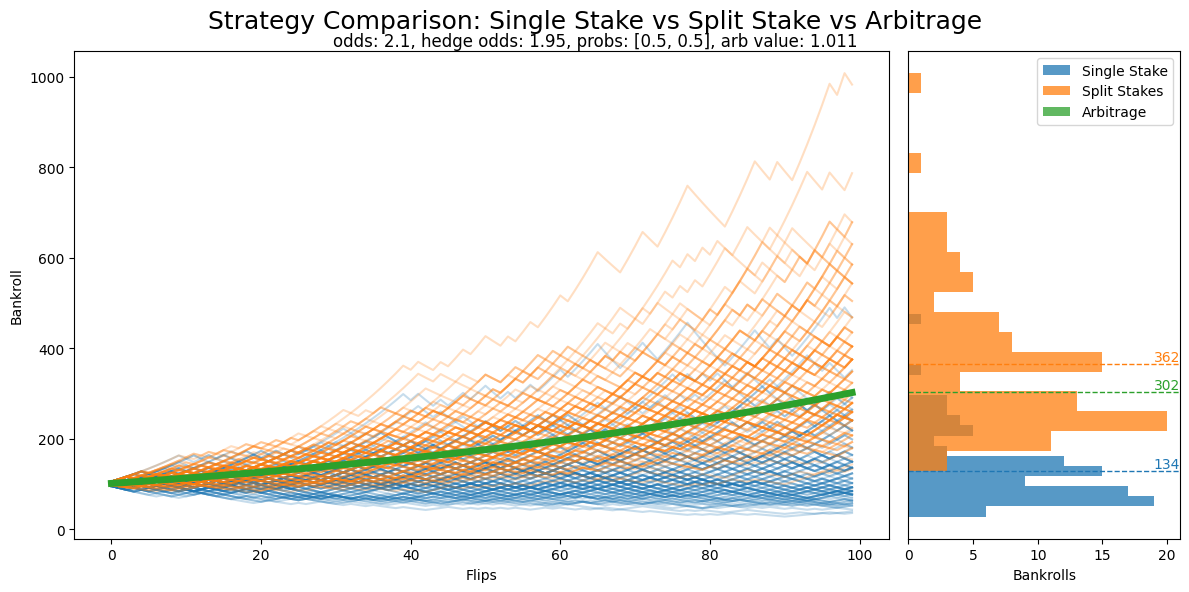
Here we see clearly that the Split Stake strategy outperforms both the arbitrage (a single line because there’s no randomness to it when we set both outcomes to pay the same amount) and the Split Stake strategy. But this short bet sequence actually doesn’t do the Split Stake strategy (or the arbitrage) proper justice. To see it in full effect, here’s 1000 coin flips intead:
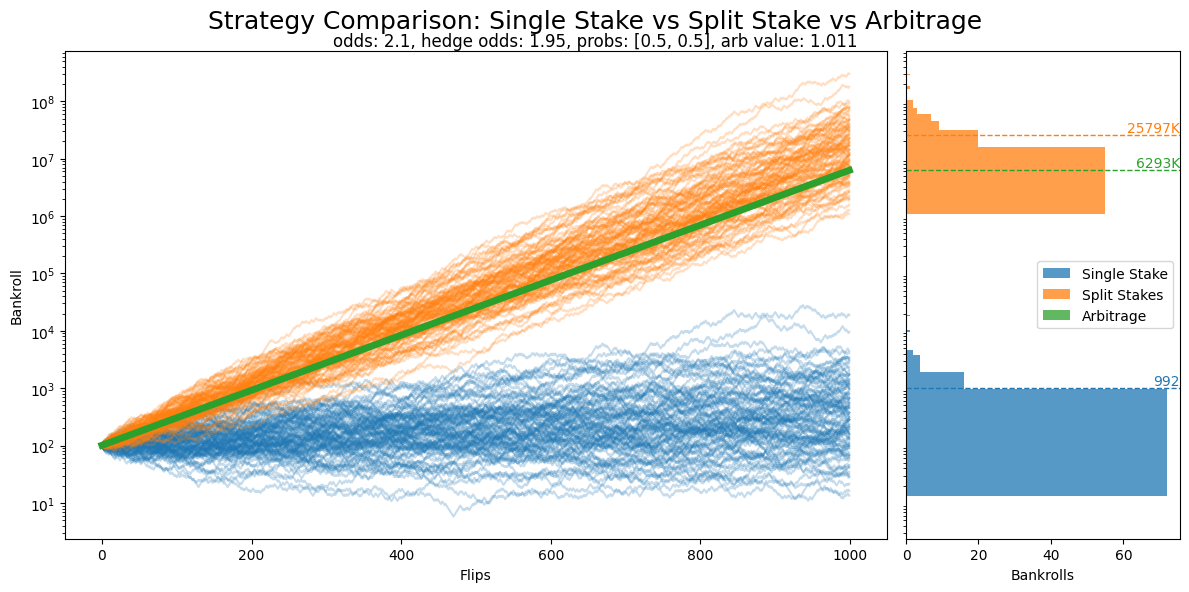
This is what Kelly had in mind when writing his paper: optimal betting positions by maximizing expected log bankroll growth, and long term compounding. The differences are so large that we now have to use a log scale to properly display the bankroll growth. We see that arbing is superior to Single Stake Kelly but what really stands out is the enormous return from the Split Stake Kelly strategy - it’s far more profitable than vanilla, Single Stake Kelly.
But as already been mentioned, this is only true when there is an actual arb available. Let’s say the mysterious man offer us 1.90 odds to hedge, what then?
First, let’s go back to this plot, now updated with the hedge odds of 1.90. What we see then, if we look close, is that the expected log bank for the Split Stakes strategy has gone down to 4.604, which is less than the best Single Stake expected log bank, 4.606. This means that when we don’t have a profitable arb opportunity, the best we can do is just bet full Kelly on the value side. Again these are small differances but let’s flip 1000 coins again with these new conditions:

We see right away that arbitrage is out of the question, as this actually isn’t an arbitrage opportunity. Overall, the Split Stakes strategy struggle to return any steady profits, while Single Stake performs just like before, as the value odds or chances of winning hasn’t changed.
It should be noted that there are other staking options available, like betting both sides but leaving out a part of your bankroll, but for making my point more easily I’ve skipped this as we know it won’t outperform the Split Stakes strategy here. But it could, if we for exampe were betting on the 1X2 market where we can find value on two out of three outcomes.
Kelly Unleashed
To briefly summarize this wall of text and numerous plots, we can say this: The Kelly Criterion aims at optimizing our long term wealth growth, by finding the staking strategy that maximizes our expected log bankroll based on our underlying probabilities and the odds on offer. This will in some cases mean using the simple formula we often see in discussions on Kelly, but sometimes it’s more complex than that and without knowing about this nuance of Kelly, we will be staking sub-optimally, missing out on fully leveraging our bankroll to achieve greater returns.
But that’s not all. By seeing gambling not as placing bets but as managing positions, there are many more example uses of Kelly’s notion of optimal bankroll growth. One aspect that ties in well with another crucial concept for successful gambling, Bayesian thinking - the simple notion that we should update our beliefs as new information comes to light - is that we can use The Kelly Criterion to update our positions! Let’s say something in our analysis changes: our projected probabilities change based on some new information, or the market moves and we are now offered different odds - Kelly can handle this and suggest new bets to make sure we are again positioned for optimal bankroll growth based on the current situation. For long-term markets like a political election or the Premier League winner outright, this can be done continuously over time.
By now you can probably suspect that the Kelly Criterion is a favorite topic of mine. Please note that I’ve intentionally left out a lot in this text to make it more readable and easier to grasp. So if you think something isn’t said here, it’s likely that I’ve just skipped it for now, but I might come back and extend the text further. In the mean time, I’m always interested in discussion so Contact me if you have anything to say.